 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MB
配点: 400 点
問題文
あみだくじは, 日本に古くから伝わる伝統的なくじ引きである.
あみだくじを作るには, まず W 本の平行な縦線を引き, 次にそれらを繋ぐ横線を引いていく. それぞれの縦棒の長さは H+1 [cm] であり、横線の端点となれるのは上から 1,2,3,...,H [cm] の位置のみである.
ここで,「正しいあみだくじ」とは, 以下のような条件を満たすあみだくじのことである.
- どの 2 つの横棒も端点を共有しない.
- それぞれの横棒の 2 つの端点は同じ高さになければならない.
- 横棒は隣り合う縦線を繋がなければならない.

縦棒 1 の上端から, 横線があれば必ずそれを通るというルールで下へたどったときに, 最終的にたどり着く縦棒の番号が K となるような「正しいあみだくじ」の本数を 1\ 000\ 000\ 007 で割った余りを求めなさい.
例として, 以下のあみだくじにおいて, 最終的にたどり着く縦棒の番号は 4 である.

制約
- H は 1 以上 100 以下の整数
- W は 1 以上 8 以下の整数
- K は 1 以上 W 以下の整数
入力
入力は以下の形式で標準入力から与えられる。
H W K
出力
条件を満たすあみだくじの本数を 1\ 000\ 000\ 007 で割った余りを出力しなさい.
入力例 1
1 3 2
出力例 1
1
以下の 1 個のあみだくじのみが条件を満たす.

入力例 2
1 3 1
出力例 2
2
以下の 2 個のあみだくじのみが条件を満たす.

入力例 3
2 3 3
出力例 3
1
以下の 1 個のあみだくじのみが条件を満たす.

入力例 4
2 3 1
出力例 4
5
以下の 5 個のあみだくじのみが条件を満たす.

入力例 5
7 1 1
出力例 5
1
縦線が 1 本しかないので, 横線をそもそも引くことができない. よって条件を満たすあみだくじは「一本も横線を引かない」の 1 通りしかない.
入力例 6
15 8 5
出力例 6
437760187
答えを 1\ 000\ 000\ 007 で割った余りを出力すること.
Score: 400 points
Problem Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw horizontal lines that connect them. The length of each vertical line is H+1 [cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H [cm] from the top of a vertical line.
A valid amidakuji is an amidakuji that satisfies the following conditions:
- No two horizontal lines share an endpoint.
- The two endpoints of each horizontal lines must be at the same height.
- A horizontal line must connect adjacent vertical lines.
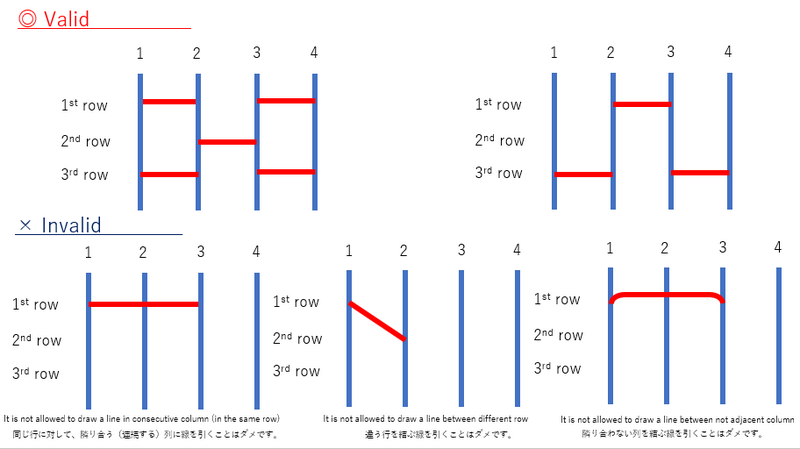
Find the number of the valid amidakuji that satisfy the following condition, modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost vertical line to the bottom, always following horizontal lines when we encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the fourth vertical line from the left.

Constraints
- H is an integer between 1 and 100 (inclusive).
- W is an integer between 1 and 8 (inclusive).
- K is an integer between 1 and W (inclusive).
Input
Input is given from Standard Input in the following format:
H W K
Output
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\ 000\ 007.
Sample Input 1
1 3 2
Sample Output 1
1
Only the following one amidakuji satisfies the condition:

Sample Input 2
1 3 1
Sample Output 2
2
Only the following two amidakuji satisfy the condition:

Sample Input 3
2 3 3
Sample Output 3
1
Only the following one amidakuji satisfies the condition:

Sample Input 4
2 3 1
Sample Output 4
5
Only the following five amidakuji satisfy the condition:

Sample Input 5
7 1 1
Sample Output 5
1
As there is only one vertical line, we cannot draw any horizontal lines. Thus, there is only one amidakuji that satisfies the condition: the amidakuji with no horizontal lines.
Sample Input 6
15 8 5
Sample Output 6
437760187
Be sure to print the answer modulo 1\ 000\ 000\ 007.